Scaling up is hard to do

Posted on by

In a recent post on schools of thought in ecology Jeremy and I exchanged several ideas on the importance of linking macro-scale patterns down to micro-scale (think population & community) processes. Jeremy correctly pointed out we need to bring this conversation back to ecology and not leave it at analogies about ideal gas laws and such.  As a macroecologist, I obviously think about this and get asked about this a lot. So here is my best thought to date on this topic.

When people discuss trying to derive macro-scale patterns from detailed processes at the micro-scale (i.e. population dynamics and species interactions), a series of obvious questions pop to mind.

  1. Can we do this scaling up?
  2. Should we do this scaling up?
  3. Must we scale up to call it good science?

I would suggest the consensus of opinion in ecology at large is somewhere between and . However, this bypasses the more basic question – can we scale up?

I am about to argue that in most cases such mapping from micro-scale to macro-scale processes is in fact basically impossible to do for simple mathematical reasons. My argument is as follows.

Imagine two scales, the micro-scale and the macro-scale. For example a 1 ha plot for mature trees is a reasonable proxy for the micro (aka local) scale. Several thousand square kilometers might be a good guess at the macro (aka regional) scale. Imagine there is a variable of interest xi,t at the micro-scale, say the abundance (or biomass) of Red Oak on plot i at time t. One can (and people have) developed detailed models for the dynamics of xi,t over time. Denote this model by the function, f, and a parameter θ representing the exogenous variables (e.g. environnment): i.e. (eq1)* xi,t+1=f(xi,t,θi,t ). But what if we’re really interested in the abundance of Red Oak at the larger, macro-scale. Maybe this is because we have conservation/policy motives (hard to imagine this crowd is interested in answers about a single 1 ha plot). Or maybe we just have a basic science interest in the regional/macro-scale. What do we do?

You should now skip ahead to the recap if you don’t like equations!

One possibility is to simply model each 1 ha plot and aggregate (sum) up the results, i.e. to study (eq2) Xt= Σixi,t where capital Xt represents the same variable (abundance or biomass of Red Oak at the macro/regional scale) and just continue to model the dynamics at the micro-scale by equation 1: xi,t+1=f(xi,t,θi,t) .This is mathematically valid. However this approach requires considerable resources to obtain data (on both x and θ) for each and every 1 ha plot and considerable computational resources to calculate a complex non-linear model for every ha. This is in practice what weather forecasting models do – but it requires supercomputers and hundreds of millions of dollars invested in data collection**. Not so easy and often in practice impossible in ecology. What else can we do?

As a short-cut is very tempting to take the detailed process based model and study it on an average 1 ha plot, i.e. (eq3a)* f(\overline{x_{i,t}},\overline{\theta_{i,t}}) (where the over bar indicates the average value) since such average data is often readily available. This model is not only data-tractable but computationally tractable because we only need to iterate the dynamic equation for one case. This is known in physics as the mean-field approach, and is a common modelling tactic. Many assume this will give the correct answer for the macro-scale problem (Xt) by summing up the average plot enough times, i.e. (eq3b) X_t=n f(\overline{x_{i,t}},\overline{\theta_{i,t}}) (where n is the number of parcels – n=100,000 in our example). However, it requires that nf(\overline{x_{i,t}},\overline{\theta_{i,t}})=\sum_i f(x_{i,t},\theta_{i,t})
or equivalently that f(\overline{x_{i,t}},\overline{\theta_{i,t}}) = \frac{1}{n}\sum_i f(x_{i,t},\theta_{i,t})=\overline{f(x_{i,t},\theta_{i,t})} (or in English that the function of the average of x is the average of the function applied to each x)

However, it is well known from Jensen’s inequality that in general it is not true that f(\overline{x_{i,t}},\overline{\theta_{i,t}})=\overline{f(x_{i,t},\theta_{i,t})} . The equality holds if and only if f(x) is a linear function or variance(xi)=0. Thus the mean-field approach fails when f is non-linear and there is variance in xi. And the failure can be quite large, not just a mathematical detail. Using Taylor’s series one can approximate the inaccuracy (known as the delta method in economics): (eq4) \overline{f(x_{i,t},\theta_{i,t})}\approx f(\overline{x_{i,t}})+\frac{1}{2}f''(\overline{x_{i,t}})Var(x_{i,t})
(where f’’ is the 2nd derivative of f – i.e. a measure of its non-linearity). Thus in systems with high variance and high-nonlinearity the correction factor can be as large or larger than the original term.

A dynamical systems context (i.e. tracking X/x over time by xi,t+1=f(xi,t,θi,t)) further exaggerates this effect because the error is compounded at each time step. And if f is a chaotic map, then deviation of the model from the true answer will grow exponentially fast due to sensitivity of initial conditions.

A quick recap: For those of you whose heads are hurting from the equations, let me summarize the action:

  1. We have a simple dynamical system modelling detailed processes over time at the micro (1 ha plot) scale given by equation 1 – we do this all the time in ecology for some variable xi
  2. We want to study the aggregate value of this variable over some much larger macro scale (e.g. 1000 km2), call it X
  3. We can figure out X by just adding up the xi overall the plots as in equation 2, but this requires modelling the dynamics of each of the 100,000 separate plots which requires detailed knowledge about each separate 1 ha plot and computational horse power.
  4. If we aren’t the weather service and can’t do , we are tempted to use a mean field approach (equation 3) modelling an average plot and then multiplying it by 100,000 instead.
  5. Unfortunately Jensen’s inequality tells us that the mean-field approach (equation 3) gives the same answer as the correct massive computation approach (equation 2) if and only if the model is linear or there is no variance in the xi. That happens sometimes (e.g.the ideal gas law models a situation with no variance), but it sure doesn’t sound like ecology.
  6. We can quantify the approximate error of the mean-field approach by equation 4 – it is the product of the nonlinearity (2nd derivative) of f and the variance in the xi;. This can be HUGE in ecology.***
  7. Putting this argument into a dynamical systems context where the error propagates forward in time, especially in a chaotic system just makes it worse

Conclusion

So if you believe ecology is essentially linear and/or has no variance then scaling works easily. Otherwise we are in the realm of weather prediction where massive data gathering and computation give rather limited understanding.

When I declare that “scaling up is hard to do” the Frankie Valli/Four tops cover of the song “Breaking up is hard to do” always pops into my head. When they sing the phrase, there is high emotion – surprise, wistfulness and maybe a bit of hope and relief. This is how I feel about the idea that “scaling up is hard to do”. All my scientific training and instincts tell me that building detailed mapping between the micro- and macro-scale is the ultimate goal. It is the signal achievement of statistical mechanics in physics. Going from the quantum mechanics of the Bohr atom to macro-chemical properties (valences, types of bonds) is the essence of physical chemistry. The power of doing this bridging is undeniable. However, I am increasingly of the opinion that in many (most?) cases, this goal is unachievable no matter how hard we try in ecology.

This in turn leaves us with the problem of what to do with all the really interesting (and real-world useful) questions at the macroscale. I only see two possibilities

  1. Declare macro-scale questions off limits because traditional methods can’t cover them
  2. Charge in to macro-scale questions and muddle along trying to invent new approaches

Personally, I can’t accept the first approach and advocate the second.

What do you think? Do you see flaws in my argument why it is mathematically demonstrable we will never scale micro-theory up to macro-theory in ecology? Can you give me a counter-example to my argument in ecology where we have something like statistical mechanics of physics where we can model from the micro-scale to the macro-scale informatively? Or if you agree with my argument, what do you think are the implications?

* I have put equation references in for the convenience of those who want to comment
** and despite all of that money spent weather prediction is still rather limited and unable to project the system forward more than about five days.
*** this approximation approach could provide a way out but I’ve never seen it attempted in ecology

51 thoughts on “Scaling up is hard to do”

  1. Interesting post Brian – I’m still trying to work my way to the end. In equation (3b) shouldn’t there be no i subscript because the average has been taken across i? Is that right?

    Reply ↓

    • Hi Amy – you are right – the average has been taken across i. I suppose it would be more clear if I replaced the i subscript with a * or some such.

      Reply ↓

    • A humorous aside, for those of us who hang around with mathematicians there are all sorts of stories of a famous mathematician attending a seminar and then standing up and leaving the room while shouting “this notation sucks!”. I think a lot of ecologists are so afraid of the equations they probably don’t realize that notation is a matter of choice and does a lot to make the math more or less understandable. This is a case in point.

      Reply ↓

      • Bertrand Russell has a great quote, something like “A good notation is almost like a live teacher. Notational irregularities are often the first sign of philosophical errors, and a perfect notation would be a substitute for thought.” I think he goes too far at the end there. But that bit about a good notation being almost like a live teacher is spot on. It very much fits with my own experience working with the Price equation, which I’ve come to think of as basically just good notation more than anything.

  2. I have two thoughts initially. Firstly, I haven’t gone through these, but I think that Kurtz 1970 and Kurtz 1971 are proofs that ODE models arise from many realizations of a Markov model. I think a starting point may be to read through Stochastic Models for Mainland-Island Metapopulations in Static and Dynamic Landscapes (2006) by JV Ross in Bull Math Biol (see this paper for the Kurtz references too). However, this isn’t the same situation as you present because the difference between the plots in your presentation is through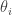 \theta_i and for a Markov model it would arise through random chance. Furthermore, the Kurtz limit theorems give rise to ODEs and you are working with discrete time.

    Secondly, do the functions f that apply to xbar (i.e. the mean value of the xi’s) necessarily have to be the same to prove that there is no way of scaling up? What if there was some different function g(xbar) that described the macroscale process? Then it is possible to scale up it just requires a more careful argument than simply applying f to xbar.

    Reply ↓

    • Thanks for the references I will follow them up.shortly.

      Your second question is a great one. Definitely no. You could just track the dynamics of X at the macro-scale – i.e. Xt=F(Xt,Θt). That is I think one of the best ways forward. But it is then no longer linked to the micro-scale. I’m fine with that but I think Jeremy (who represents many people I’ve spoken with of like mind) might not be. There might be some middle ground where you could try to study links between f and F or θ and Θ. But as my “proof” shows, these links will have to come de novo, not from some automated scaling process.

      Reply ↓

      • Thanks for the response. I was thinking that f and F could be linked without necessarily having to be the same. Here’s an example that isn’t micro to macro, but it’s an example about links being possible w/o functions needing to be the same.

        N_{t+1} = N_t(1-d \Delta t) + N_t b \Delta t (1-d \Delta t)

        can be linked to:
        \frac{dN}{dt} = (b-d)N

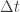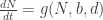        by way of taking the limit as \Delta t goes to zero. There is a link, but N_{t+1}=f(N_t, b, d) and \frac{dN}{dt} = g(N, b, d) are not the same. The top equation assumes the order of events are births first, then deaths.

        But then again my example is kind of sneaky and it’s not about taking averages, so you might be right to require that both f’s are the same.

      • Hi Amy – a great example. Thanks for adding it. I think that is exactly the kind of thing everyone (including me!) hopes we could do. I am fine with F different than f – the key point is if we can have a formal mathematical link (as in your example) or not (as in my proof).

        Looking at your example, it seems to be the exception that proves the rule. You are scaling in space instead of time, but that doesn’t matter. However you are linear in your state variable (here Nt instead of xt) AND you have no variance (e.g. replicates of N across space or even just letting b and d vary over time). My post definitely requires BOTH non-linearity AND variance.

        Thanks for a great clarifying example!

      • @ Brian: Oh, I’m actually fine with that sort of thing in many cases. Just so long as the wrong conclusions aren’t drawn. I get annoyed when somebody has a macroscale dynamical equation that isn’t derived by scaling up from the microscale, and infers from that that the microscale is somehow unimportant, or that the macroscale is totally independent of the microscale.

  3. Hi Brian,

    My questions for you come up at the very end. Yes, scaling up is hard–but what *exactly* do we do in light of that? You say you “refuse to accept” that some problems might just be intractable. That sounds to me like King Cnut refusing to accept the incoming tide! Can you elaborate on how exactly we “muddle through” in the kind of situations you describe, perhaps by reference to some real macroecological examples?

    I don’t want to comment further until I have more of a sense of what “muddling through” amounts to. In particular, “muddling through” can’t involve somehow estimating f(x,theta) or some approximation to that function, can it? As that would mean that you do actually know something about how to scale up or scale down. As you know from my old posts, where I think macroecologists have sometimes run into trouble in the past is where they’ve mistakenly claimed or implied that they could do something like that.

    Reply ↓

    • Hi Jeremy, I am eager to discuss this in detail with you . It is the discussion lurking under many of our back-and-forth comments for some time.

      Science is a blend of knowing the “art of the possible” (e.g. Medawar) and of taking risks and going in new directions. I hardly think having a bit more of risk-taking bent makes me King Cnut! I also think science (at least some subset of scientists) has an obligation (morally and financially) to step up and tackle problems that are useful (though don’t want to derail this into a basic vs applied research debate as I favor both).

      Now as to routes forward (which I some what tongue-in-cheek called “muddling”)
      1) There is still pretty high power in simply studying things empirically and just finding patterns at the macro-scale.
      2) You and Amy both suggest studying things simply at the macro-scale. (the function g in Amy’s comment or F in my reply). This to me is the obvious route forward. Indeed I see it as a very “high quality” science route forward. All I’m saying is all the people out there (they are legion) who say this is bad science because it isn’t reductionist enough or doesn’t anchor in the “right” scale of populations are never going to be satisfied.

      I of course agree with you Jeremy that for macroecologists to then claim that they have reached down is wrong. Do you have specific examples in mind?

      In short, I think macroecology is doing just fine by identifying macro-scale patterns and then using macro-scale processes (e.g. evolution, sampling, species interactions of a fundamentally different nature than the pairwise, individual Lotka-Volterra–assumption-like-interactions) to explain them.

      But for those saying this is not good enough, and that we have to find links down to a more “fundamental” level of populations (or physiology), this post is my official statement that it is NOT GOING TO HAPPEN (because it can’t) so either: a) get honest that your view is so narrow that only one level of processes is acceptable and you consider the only good science to be science that bridges to your favorite level/scale, or b) adjust and allow macroecology to exist as it has doing good science even without those bridges.

      If you feel heat coming out of these words they are not directed at you Jeremy (who I’ve always considered an interested and intellectually honest thinker in this area) but to the literally 100s of people I have had conversations with who are thinking shallowly about this.

      Reply ↓

  4. Brian,
    Really interesting post. This is nowhere near my area of expertise, but it brought several things to mind that I’ll just toss out there.
    1.) You’ve convinced me based on the mathematics about the scaling up, but are you arguing that understanding any link between the micro and macro is impossible? If we’re not talking about scaling up, but rather modeling the link as its own separate (highly complex) function, isn’t this possible (or is this the same as Amy’s question)? Isn’t the “muddling along” what’s been done in the climate and weather fields? We’ve attacked the questions of weather and climate as two separate fields of study. From that, we now have a relatively good handle on local weather patterns on short time scales, and we’re getting a better handle on macro-scale climate science, but the link between the two has not been well established. But now that we have a better handle on both, scientists are trying to make the links between broad-scale climate change and local weather events using retrospective type analyses. Could we eventually get to a similar place in micro- and macro-ecology?
    2.) Does chaos theory offer any solutions? (I’m way behind on that field, since the last book I read on the subject was James Gleick’s book from nearly 20 years ago, so this question may be moot.)

    Thanks for the great post.

    Reply ↓

    • Thanks for the comments and questions.
      on #1 – I agree that we can model things at the macro level as Amy & I discussed (I should just call this equation 5 – Xt=F(Xt,Θt) ignoring links to the micro. And we may, occasionally in special circumstances (i.e. linear or no-variance) be able to build bridges to the micro that can be informative and maybe reassure us that we are not completely untethered (as per Amy’s example). I find weather/climate a great analogy. They basically have the money to do do equation 2 (parameterize & initial conditions on every grid cell then compute the model). But they still do equation 5 too. And they are extremely comfortable with correlations as well. I always point to the recent development of teleconnections (ENSO, PDO, North Atlantic Oscillation, etc) as an example. These are serious macro-scale patterns (half the globe, decades of time). And THEY WERE DISCOVERED AS CORRELATIONS. The story of ENSO is a bit longer, but many of the teleconnections we have today came out of a giant principal component analysis (called EOF by them) on historical weather data – i.e. an exploratory model – no mechanism in sight. This then has led to macro-scale models (equation 5 approach) that explain what is going on at the macro-scale. But the micro-scale (equation 2) approach is so complex it is hard to understand how they produce these patterns. So I claim that climatologists are basically blazing the trail for us macroecologists. They just don’t get as much grief because they have THE micro-scale model (equation 2) completely worked out (7 equations of basic physics) and they recognize the severe limitations of it. 😉

      on #2 – I personally think the main end result of chaos is that it is ergodic which is a fancy way of saying that there is a predictable probability distribution (aka histogram) of where the model goes either over time or over many replicates (ergodic means the two cases are equivalent). Thus to me the main message of chaos is that if we want to go to more than a few time steps ahead, we have to look at probability distributions of state variables, not differential equations.

      Reply ↓

      • Your first paragraph raises a whole number of interesting questions wrt this topic.
        For instance, one of the problems with the “macro” approach is that it glosses over variability–either temporal or spatial or both. Using climatology vs meteorology as an example, this basically means that neither science, in their current states, has much chance of predicting for example, extreme events, such as the droughts in Russia or North America over the last few years. Their prediction requires detailed and specific physical understanding that most climate models don’t contain, and they are far too persistent to be predicted with weather models, which only go out a week or so. It’s a serious no-man’s land with huge practical consequences. I’m by no means convinced that discovering what really drives these events in no-man’s land will happen by working down from the macro-scale–especially for temporally quick events (e.g. storms). It’s still an enormous challenge.

      • Good point! There are some real no-mans lands in weather/climate which should be a bit humbling to us here in ecology. As per my last reply to your other comment, I do think the 3-6 month predictions have gained more from the macro than the micro-scale which is relevant to our discussion here although it is important to highlight how much work they still have to do. A climatologist I worked with at Arizona that I respect used to say 5-10 year weather predictions were on the horizon (10 or 20 years from now). But maybe that was wishful thinking.

    • “I do think the 3-6 month predictions have gained more from the macro than the micro-scale”

      No question about it, and it is a good supporting piece of evidence for your argument. And I should add that storms (my example) are somewhat predictable with weather models, depending on spatio-temporal scale of interest and error tolerance. For example, predicting specific locations of tornado occurrence, a huge challenge, is much, much! more likely to come from improvements in meteorological models than from climate models.

      Reply ↓

  5. Hi Brian,

    great topic!

    You were invoking the comparison to other disciplines such as physics or weather forecasting, where physics could be seen as the more successful example and weather forecasting (maybe) as the less successful example of upscaling. What’s the difference between the two?

    I would say that in weather forecasting, there are a few very local processes about which we are certain, governed by the Navier-Stokes equations, and weather models (an to some extent climate models) aim to scale up from a gridded version of this processes to a potentially very large scale. This leads to the known problems of nonlinearities, chaotic behavior, sub-grid heterogeneity, etc. for which we have no truly satisfying correction. It seems to me that you are thinking about our ecological upscaling problem in this way.

    If we look at physics, however, this is not how it works. Physics does not work as one big equation that is scaled up from the elementary processes to the global scale. Rather, we have some natural scales such as the elementary particles of the standard model, which then build up the hadrons (Protons etc.), which then build up the atoms, which then build up molecules, gases, fluids and solid materials, with theories that translate processes at the smaller scale to phenomena at the next larger scale. There is no physical theory that goes directly from elementary particles to, say, solid matter. Rather, people are satisfied to understand how crystals are build up from atoms, and how atoms are build up from smaller particles, etc.

    So, what I wonder: the problem that we have to solve in ecology, is this really of the “weather forecast structure”, or is it rather like physics, where we want to understand how individual behavior and reproduction makes up populations and communities, and how communities make up ecosystems, and how ecosystems or communities evolve over time and in space, and wouldn’t that be a much easier question to solve than the problem you pose? Or in other words, we may not have to scale up from the smallest to the largest scale in one step, but we have find “appropriate” intermediate steps and understand the transitions between them. In physics, this separation of scales works so well because physical systems have a very strong organization, in the sense that you can very well work with the concept of a proton without caring at all about the fact that, within a proton, there are smaller things going on. In ecology is certainly less so, but is it impossible to find sensible higher units than the individual that allow us to scale up in “steps”? People who say you have to scale up directly from the individual level probably say “no”. I’m not sure, but I feel inclined to think that we can separate some scales, but we have to think about how to do this. Would be interest to hear what you think. Because, after all, if one wants to build a causal theory of macroecology, this theory must sure be build in terms of processes that are at a smaller scale than the macroecological pattern, mustn’t it? So, what would be the natural scale for formulating a causal macroecological theory?

    Reply ↓

    • Hi Florian. Really nice points that I agree with. Your thoughts deserve more time and I’ll come back to them, but as I’m dashing off to a meeting – briefly:

      Can I say that ecology has components that are like physics (population dynamics, physiology) and components that are like weather (macroecology) and some that are in the middle (community ecology)? And that we cannot build profound deep bridges from the physics-like regions to the weather-like regions (this will be the controversial statement)?

      This is an interesting question – do we need processes that map to things lower down in the hierarchy or do we need processes that are at the same level as what we’re trying to model. The assumption is always the former. But population dynamics models things in terms of birth rates (which is a population process – yes it comes from individual births – but when you have a birth rate of 2.3 you are now talking about a population level parameter). I think this “look below” for mechanism is the source of much trouble! I think macroecology needs processes that are at macro-scales.

      Reply ↓

    • Just to expand on my earlier thoughts …
      1) I really like your highlighting that physics has natural scales (proton, atom, molecule). Biologists like to think about biology having natural scales too, but between cell and individual it is a stretch to say there are natural levels (people talk about tissues or organs but these are not well defined units, especially in plants) and between individual and the whole globe where is there a natural break? Community ecologists have more or less admitted that the scale of a community is arbitrary. I have claimed with a philosopher collaborator (Angela Potochnik) that thinking biology has natural levels is a disservice and even misleading (also multiple references of others arguing this can be found therein). Personally I think this may be one major reason ecology can’t link between the scales like physics has.
      2) I think the second reason ecology can’t link between the scales is the variance. Under my model/”proof” nonlinear doesn’t prevent scaling up if there is no variance. Many things in physics have no variance (physicists would be frightened if protons varied in weight, from a chemical interaction point of view all carbon atoms are the same, etc). Some might point to statistical mechanics which deals with the molecules having different velocities/momentums but this is a bit of a cheat because they then study the macro-scale property of temperature which by definition is the AVERAGE momentum (and those molecules are identical in all meaningful features other than velocity). I know this is nonsensical but if physicists could figure out what the velocity of the whole gas is knowing just the velocity of the individual atoms that is what would be comparable to what I am talking about and we are attempting in ecology. In short – I think physicists deal with a lot less variance between entities than ecologists and that makes a bigger difference than one might think.

      Reply ↓

      • Hi Brian,

        no idea how you’re managing with all these replies … hence, just a few short thoughts:

        1) agreed, it’s difficult to identify natural scales in ecology, although I would say that at least the individual is a natural unit, problem is that it doesn’t act at the same scale for all species – may be that for plants really everything above the individual is essentially without a natural scale. For animals that have a strong organization structure, higher level description also make sense to me.

        2) hmm … I have to say I don’t see why variance in particular poses such a fundamental problem to creating a “statistical mechanics” of ecology – sure, you have to deal with it mathematically, but I don’t see why one couldn’t solve the type of problem that you pose above with sufficient accuracy to make good predictions – given that the probability distributions are known, it’s just about solving a lot of integrals, isn’t it. I would actually think that interactions and dispersal are the more tricky problem to scale up. Btw., I believe when deriving thermodynamics from statistical mechanics, you do not work with the average, you work with a distribution (Boltzmann) of velocities, so it’s actually a quite similar problem.

  6. For what it’s worth, Iwasa, Levin, and Andreasen wrote about just this problem in 1989: “Aggregation in model ecosystems II. Approximate aggregation,” IMA Journal of Mathematics Applied in Medicine and Biology, 6, 1–23. The paper asks, given a definition of how to get the macro variables from the micro variables, what is the most accurate form for the dynamics of the macro variables? (The authors point out that “most accurate” can have different meanings, depending on what one wants to preserve. They take the measure of inconsistency between two dynamical systems to be the norm of the difference between the vector fields, weighted by some function w that allows one to insist on more accuracy in some variables than in others.)

    It’s not easy to read and the results aren’t easy to use, but it’s nice to see people tackling this issue head-on.

    Reply ↓

  7. Haven’t read the comments yet but I agree that it’s really quite difficult to scale processes up.

    An additional reason is that, even if you opt for the computation intensive, weather prediction modeling approach, it’s a different story in ecology. Different as in “worse”. In weather modeling/forecasting the physical determinants, as defined by the Navier-Stokes fluid dynamics equations especially, are based on just a few well known processes, especially the interactions of pressure and humidity and momentum. The predictability breaks down after a few days, due to insufficiently accurate initial conditions, as you state. And the weather forecasters try to address this chaotic result by continually assimilating new data on the relevant state variables and re-predicting the next week out. But in ecological systems, you have that issue, but you also have poor or entirely lacking understanding of the determinants of the system itself. That is, we have no set of equations analogous to the Navier-Stokes equations, and all kinds of things happen on all kinds of time scales, that are poorly represented in the models if at all.

    In short, more variables, poorly understood, plus chaos.

    Reply ↓

    • Hi Jim – I completely agree. I figured I was making a bold enough argument already, but I agree that ecology is fundamentally (qualitatively?) different than weather because there we know the equations – they’re just chaotic. On the whole I think that has been a blessing for weather/climate as it has freed them to move beyond the search for the right question to how to do things at the macro-level. As I noted in my comment on teleconnections they have managed to do somethings by a combination of correlation/pattern searching and macro-scale modelling. Our 3-6 month predictions are improving because of this.

      And I agree not only do we not know the equations for ecology (unlike Navier-Stokes for weather), but there are certainly a whole lot more of them. This “multi-causal” aspect of ecology makes it very different from say physics and I think much more interesting!

      Reply ↓

    • That is one of my favorite papers.

      I think there is an interesting distinction between looking for mechanism for macro-scale in populations vs looking for mechanism in physiology. I have long argued that macroecology needs to skip a level (populations) and look at physiology. I don’t have anything formal to justify this – just intuition and experience. But it is unarguable that a major macro-scale phenomenon is climate gradients and physiologists spend a lot of time telling us about responses to climate. Population biologists have not (although maybe they could, and the lab Jeremy came from and Jeremy’s own work is a notable exception). Total speculation is that physiology will ripple up and still have a signal at macroscales to a greater degree than population biology. Certainly the 3/4 metabolic scaling that is held up as a major success of macroecology follows this template.

      Reply ↓

      • And just to clarify my last comment – no I haven’t just undone my whole argument. I am still advocating the main route forward is the “equation 5” approach of modelling macro processes. Its just that I think physiology serves as constraints on evolution and as a key determinant of outcomes of climate variation – two of my major candidate forces for macro-processes so it is “sneaking in the back door”.

      • No, I understand. I’ve never understood why the population biologists were so divorced from physiological ecology and environmental constraints in general. Or so it has seemed to me, maybe my impression is wrong or biased.

  9. Fun post Brian, thank you. I have one comment and a few references to throw in.

    I think the value of your macro-scale muddling approach depends on whether your objective is prediction or understanding mechanisms. If regional scale prediction is the goal, as in many conservation applications, then focusing primarily on the regional scale patterns is the way to go. I think macroecology is tremendously undervalued for its predictive/applied value. On the other hand, if basic understanding is the goal, then scale-bridging may be more important. My impression is that macroecologists most often elicit the pissed-off reductionist response when they try to infer process from pattern, and especially microscale processes from macroscale patterns. The neutral theory debate (species interactions inferred from patterns of abundance) is just the most recent “classic” example.

    As for the references, the “perfect plasticity” papers that Pacala’s lab has been turning out are a fascinating example of really clever approximations. They are scaling from individual trees to communities, not from populations to regions, but their results offer a ray of hope that scaling-up may not be impossible. In order to figure out this approximation, I think they first had to go all the way to the reductionist extreme with computationally-intensive, individual-based forest simulators. Here are two papers that I liked, with the real meat in the Strigul paper (which was surprisingly accessible for my remedial math level):

    Purves, D., J. Lichstein, N. Strigul, and S. Pacala. 2008. Predicting and understanding forest dynamics using a simple tractable model. PROCEEDINGS OF THE NATIONAL ACADEMY OF SCIENCES OF THE UNITED STATES OF 105:17018–17022. doi: 10.1073/pnas.0807754105.

    Strigul, N., D. Pristinski, D. Purves, J. Dushoff, and S. Pacala. 2008. Scaling from trees to forests: tractable macroscopic equations for forest dynamics. Ecological Monographs 78:523–545. doi: 10.1890/08-0082.1.

    Finally, you mentioned that you weren’t aware of the delta method approximation approach used in ecology. I think you meant in the context of spatial scaling from site to region? Here are a few papers that apply the tool to somewhat different ecological problems (forgive me for including my student’s recent paper):

    Ruel, J., and M. Ayres. 1999. Jensen’s inequality predicts effects of environmental variation. TRENDS IN ECOLOGY & EVOLUTION 14:361–366. (This one is a review)

    Benedetti-Cecchi, L. B. 2008. Neutrality and the response of rare species to environmental variance. PLoS ONE 3:e2777.

    Hsu, J. S., J. Powell, and P. B. Adler. 2012. Sensitivity of mean annual primary production to precipitation. Global Change Biology 18:2246–2255. doi: 10.1111/j.1365-2486.2012.02687.x.

    Reply ↓

    • Thanks Peter. Good points. And I really appreciate references – I hate it when people vaguely imply something is out there without the details.

      I whole heartedly agree that using macroecological patterns to imply that one has the right micro-processes and therefore supports a particular model (e.g. neutral theory) is completely fallacious. This may be what Jeremy meant about macroecologists claiming they have scaled down. I’m not sure whether it is macroecologists or microecologists (neologism alert) who do this. I suspect a bit of both, but it is wrong whoever is doing it.

      I like the perfect plasticity papers. I’ll have to think about how they apply to this scaling argument.

      I did mean that I hadn’t seen the delta method applied to scaling (I know for example of its application to bet-hedging), but its great to have some more references for myself and the other readers. I just printed out the Hsu et al paper last week and its already in my to read list! Anything that increases the use/awareness of Jensen’s inequality and the delta approximation in ecology is a good thing as far as I’m concerned.

      Reply ↓

    • I, and I think most macroecologists at this point, completely agree with your point about making inferences with respect to micro-scale processes. However, your comment goes a bit further than that to state that:

      “On the other hand, if basic understanding is the goal, then scale-bridging may be more important.”

      I suspect that what you mean here is that if we want a basic understanding of specific kinds of micro-scale processes that many ecologists find interesting then we need scale-bridging approaches. If so, I think it’s important to be clear about that. If not, then we disagree about whether macroecology can yield “basic understanding”, and I’d suggest that you take a look at McGill & Nekola (2010).

      McGill, B. J. and J. C. Nekola. 2010. Mechanisms in macroecology: AWOL or purloined letter? Towards a pragmatic view of mechanism. Oikos 119: 91-603. http://dx.doi.org/10.1111/j.1600-0706.2009.17771.x

      Reply ↓

      • Yes, I was being vague with my “may be important” comment. You’re totally right that not all important mechanisms and processes operate at the micro scale, and that many important (and interesting!) processes operate at the macro scale. I like McGill and Nekola’s call for pragmatism. The burden should not fall entirely on the macroecologists either. “Microecologists” should prove, and not simply assume, that the processes dear to their hearts are important at the macroscale. Jeremy has been good at this.

      • For readers who don’t speak Italian, Ethan’s comment “Va bene” translates as “Yes, Jeremy Fox IS good, isn’t he? And good looking too!” 😉

    • This is just fascinating. Thanks so much for this discussion, everyone. Brian (and everyone, but especially Brian), I’m not sure how you have time to do this… but thank you!

      I want to echo some of Florian Hartig’s thoughts above about “natural” levels of organization in physics and biology.

      First, the point in physics isn’t to have a grand mathematical theory of everything. It would be cool if it existed, but it probably doesn’t exist in a way that we can mathematically understand (yet). I think that the same is true of ecology. There probably is a way of writing everything down in one equation, but we certainly don’t have that yet. But I would suggest that a system of equations isn’t really the point. Physics is perfectly happy, productive and useful with different sets of equations that tell us how a building collapses versus how to build a solid-state hard drive. Perhaps someday it will be possible to use quantum electrodynamics to explain plate tectonics, but in the meantime we’re doing pretty well without such a unifying theory. Likewise, I don’t think that using the dynamics of protein folding to explain predator-prey dynamics would be particularly informative. Of course, I’m building several straw men here, but I hope you understand my point: each equation or set of equations is just a heuristic to help us understand some part of the universe, and we shouldn’t be surprised or disappointed that we rely on different heuristics in different contexts.

      Second, not to get too deep into some of last week’s conversation about schools of thought, paradigms, Kuhn, Lakatos, etc., but I don’t think that we ecologists should be concerned about the arbitrariness of the scales at which we ask questions. Scales are arbitrary and subjective in all sciences, including physics. We think that “atom” is a real and objective level of organization, based on most of our daily experiences, as well as a huge body of scientific work. But, of course, atoms are just a great approximation of the behavior of systems of subatomic particles. People choose to talk about atoms as though they’re real because it’s an extremely useful heuristic for describing and predicting the universe. Likewise, a plant community isn’t a phenomenon that has a clear delineation in every context, but it’s still something that most people can easily recognize, and that is extremely useful for describing ecosystems, landscapes, etc. I mean, heck, even an individual organism is actually an ecological community (http://www.sciencemag.org/content/336/6086/1255.abstract), but we don’t model growth of an individual cow by simulating the dynamics of the microbial communities in its gut and on its skin (although I sure would like to!), nor by predicting transcription, translation and protein folding in every cell of its body.

      All of that said, I’d like add one more citation to those above, which has been among my favorites for a while:

      Moorcroft, P. R. 2006. How close are we to a predictive science of the biosphere? Trends in Ecology & Evolution 21:400–407.

      Thanks so much for all of the citations above. I have a lot of reading to do…

      Reply ↓

      • Thanks Gabriel. I pretty much agree with everything you said, so I won’t waste electrons with a long reply. But I wanted to pull out a quote from what you wrote because I think it is a very nice summary of my thoughts, namely:

        each equation or set of equations is just a heuristic to help us understand some part of the universe, and we shouldn’t be surprised or disappointed that we rely on different heuristics in different contexts.

        ^Yes!

  10. Hi all,
    Great post and discussion. I’m going to echo Peter’s thoughts and offer a slightly earlier reference. Richard Law and colleagues have shown how to scale up from individual to population processes (see also here), including stochasticity and non-linear functional forms describing births, deaths and movement/dispersal, which can lead to linear (logistic) population level behaviour under some specific circumstances (Roughgarden, Royama and others have also shown how to do this elsewhere in books). I haven’t read the later Purves & Pacala references Peter mentioned yet, but if they’re related to their earlier zone of influence (ZOI) stuff, then I think they’re also related to the Law et al refs.

    By understanding certain features at a ‘micro-‘ scale (in this case, individuals), we can predict what’s going to happen at a ‘macro’ (population) scale and also understand when and why those predictions fail (when & why ‘spatial logistic’ population growth isn’t really following logistic assumptions). So a useful question might be what’s different about the scaling up in Brian’s example compared to these? Or am I oversimplifying/getting completely the wrong end of the stick?

    Reply ↓

  11. Two thoughts. First, one of my favorite pieces on the scale transition issue is PW Anderson’s “More is different” (http://www.physics.ohio-state.edu/~jay/880/moreisdifferent.pdf) – a perspective that argues that simple local-scale models may never be able to transfer to global scales. It is quite old but I am interested in your thoughts on his perspective.

    Second, I think the fundamental issue that is not being addressed is the issue of data, and the will to get it. Suppose that macroecological questions truly do need more data, at more scales, than can ever be obtained from a small set of local-scale plots. If this were true, then all the effort in the world would never be sufficient to generate broad-scale understandings, and we would have been better off spending time making more measurements, articulating the need for more funding, etc. To what extent do you think big ecological questions require big data, bigger than we have? And should we not, as a community, be making the case for getting it?

    Reply ↓

    • Good points and thanks for the reference.

      I think if we are going to go the route of Equation 2 (aka the weather forecast model where we model every grid cell separately) then the data availability problem is much bigger and harder than the computational tractability problem. LIke most campuses, Maine has a cluster that is always growing despite being underutilized.And if I’m not trying to do real-time prediction like weather, then I could get enough cycles for almost anything. But trying to get the data to parameterize each of those grid cells is not going to happen. I guess the question is whether going this equation 2/weather route is something we want/need to do in ecology. Basically the global digital vegetation model people are trying to go this route (the purves & pacala work as well as a paper by Moorcraft have all been brought up in this thread). I personally think we can go the route of equation 5 – models at the macroscale. If true we can breath a sigh of relief – its a lot cheaper than trying to create the National Ecological Service (a la the National Weather Service) with massive sensor networks (given that NEON is going to cover ~20 sites at $100 million, the prospects of going down the big data to parameterize models route scares me).

      Reply ↓

  12. NSF is currently funding programs under a Macrosystems grant, where the projects actively try to bridge scales, be they temporal or spatial. Obviously the problems you state exist for most of these projects, ours is trying to bridge short term carbon flux measurements and milennial scale changes in vegetation, which is obviously difficult, but as new analytical techniques become available, and particularly with the development of more robust data assimilation techniques these problems move from the intractable to the difficult.

    The upshot of the Macrosystems grant is that there are now a bunch of research groups in the US interested in linking continental scale ecological processes to interactions at more local scales. As far as I know there’s also a special issue of Frontiers in Ecology and the Environment coming out in the new year that details the issues faced by these projects and the approaches taken.

    Reply ↓

  13. Hi Brian,

    Thanks for a great post and awesome discussion!

    I do understand your position on studying macro-scale patterns using macro-scale processes. That would be the ideal way to go, however the problem of getting the data describing these processes is a bit puzzling me…

    On the other hand, I think there are examples in ecology that employ the eq. 4 in your post to model from micro- to macro- scale:
    – Bergstrom et al. (2006) used the moment approximation method to up-scale the dynamics in a predator-prey system from the laboratory scale to the field;
    – Melbourne and Chesson (2006) and Englund and Lenardsson (2008) also apply this approach, which they call “scale transition theory”. Melbourne and Chesson (2006) up-scaled the periphyton growth from the rock-scale to the stream scale by including the spatial variance of periphyton density and spatial covariance for periphyton and grazer density in addition to the mean-field approach. Englund and Lenardsson (2008) used the data on the consumption of prey by predator, which were collected a) in the laboratory and b) at a small-scale field level, to compare the performance of scale-transition theory against the empirical data collected at regional (300 km2) scale. They concluded that the data collected at a small-scale level in the field gave a more realistic approximation compared to the lab data, especially at high prey densities.

    Please correct me if I am getting something wrong here and those studies are not doing what you have described.

    I of course can understand that these examples are probably not exactly what you were looking for as a macroecologist, as they stop at the two-species system and do not go further than that, however they already are a demonstration of a possibility to apply the moment approximation method to ecological systems.

    Thanks again for raising this issue!

    Bergström, U., G. Englund, and K. Leonardsson. 2006. Plugging space into predator-prey models: An empirical approach. American Naturalist 167:246-259.
    Englund, G., and K. Leonardsson. 2008. Scaling up the functional response for spatially heterogeneous systems. Ecology Letters 11:440-449.
    Melbourne, B. A., and P. Chesson. 2006. The scale transition: Scaling up population dynamics with field data. Ecology 87:1478-1488.

    Reply ↓

  14. I just wanted to follow up on some of the references people have been giving (thanks!). Some of them are just commentaries, but there are six papers specifically suggested as involving scaling up:
    1) Two by Purves & Pacala et al on scaling up the individual based forest simulator SORTIE using the perfect plasticity assumption (PPA) suggested by commenter Peter Adler
    2) A paper by Richard Law, David J. Murrell, and Ulf Dieckmann suggested by Mike Fowler
    3) Three papers by Viktoriia (two by Leonardsson and colleagues, one by Chesson and colleagues which actually stands in for several by Chesson).

    First these are all excellent papers. I already knew and very much liked #1, #2 and some different papers by Chesson in #3. The ones by Leonardsson are new to me.

    My basic summary result is that they all fit in the framework I laid out and none accomplished the thing I claimed as impossible.

    #1 and #2 both start with an individual based model (SORTIE tree IBM or an individual simulation of logistic-like growth). This is my equation 1. They run these individual level models. They then define the macro-scale variable N (total abundance across space). They define dynamics for N (or Nbar i.e. average N or density). This is effectively my equation #5 – i.e. macro-scale dynamical model (F) for the macro-scale variable. These macro-scale equations DO use parameters from the micro-scale dynamical model (f), i.e. relate Θ to θ but they DO NOT actually derive the macro-scale model (F) from micro-scale dynamics (f) which I claimed impossible. Indeed if you look their micro-scale and macro-scale models are very different (and no claim is made that the form of F follows directly from f).

    Linking parameters is a very nice accomplishment and I don’t in anyway want to belittle it. I do note that these are scaling from the individual to the population (slightly different than what I was envisioning). More importantly I think there is a twist in each case. The Law paper uses what are basically population level parameters (birth rate, death rate which are not truly individual properties) in the individual level model so, without taking away anything from their accomplishments or elegance, it is not profoundly surprising they are able to carry these parameters up to the population level. The PPA papers do the opposite – they use individual parameters (ontogenetic growth) and carry these into the population model, however, they do this by making the Perfect Plasticity Assumption which is very clever and a great solution to their goal, but it effectively removes all spatial structure from the model – it effectively models all trees as growing at one point.

    #3, as Viktoriia suggested do indeed use my equation #4 – IE they use the variance and nonlinearity in a correction term derived from the delta method. As I mentioned this seems like a promising step forward. They all do this in a context of perfect spatial homogeneity (basically θ is not subscripted by i or varying across space) and look at the endogenously generated spatially generated dynamics.

    So in summary these papers use one of the two methods I suggested for macro-scale models – either using macro-scale dynamics (F) or using the delta approximation to scale-up micro-scale dynamics (f). None of these papers do (nor claim to do) what I claimed was impossible: scaling up a non-linear micro-scale dynamical model in a context where there is exogenous spatial heterogeneity (in contrast to the internally generated spatial variation of the papers in category 3). In principal, as I noted, the delta method (equation 4) COULD be used in this context but I haven’t run across it yet.UPDATE Robin Snyder has reminded me of some more papers (which I should have remembered as I studied them carefully when they came out) such as a nice one by herself and Chesson . While my now deleted statement is true, its more a reflection on my poor memory of the literature and the issue of endogenously vs exogenously generated variance is irrelevant. So I’m going to back off any claims of what has or has not been done in the literature since I clearly am doing a poor job of retaining even what I’ve previously read in my head. I am instead going to resummarize that – as claimed in the original post – there are three ways to scale from a micro-scale model to a macro-scale model (equation 3 is still wrong unfortunately):

    1. equation 2 – model at the detailed scale at great computational cost and worse data collection requirements (aka the weather approach)
    2. equation 5 – model at the macro-scale (F) (and if lucky get some linkage between the micro and macro parameters but not the actual models f and F)
    3. equation 4 – Use the delta approximation. This is what I personally have learned most from commentors is how much more widely this has been used than I knew/remembered. The only thing I’ve seen it used on is scaling up population dynamics (state variable x is abundance, i.e. N)(and again that is probably a reflection of my knowing a limited subset of the literature). But that doesn’t mean it couldn’t be used on some other state variable. It probably should. It is an approximation and I would be curious to see how well it works on something other than abundance.

    This has been a very informative discussion that I have learned a lot from. Thanks for the many wonderful comments.

    Reply ↓

  15. Pingback: Scaling up is hard to do: a response | Dynamic Ecology

  18. Pingback: Friday links: Nature editor vs. blogger, how to teach what you don’t know, and more | Dynamic Ecology

  19. Pingback: Book review: Community Ecology by Gary Mittelbach, and Community Ecology by Peter Morin | Dynamic Ecology

  20. Pingback: Steven Frank on how to explain biological patterns | Dynamic Ecology

Leave a Comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.