Ecologists need to do a better job of prediction – part I – the insidious evils of ANOVA (UPDATED)

When I teach a graduate statistics class, I spend some time emphasizing that most statistical analyses can produce a p-value, an effect size and an R². Students are quick to get that p<0.05 with effect size of 0.1% and R² of 3% is not that useful. This is not a particularly novel insight, but it is not something many students fresh out of a first semester stats class realize where all p-value all the time is emphasized. All 3 statistics have their roles. p-values are used in a hypothetico-deductive framework telling us the probability the signal could have been observed by chance (does nitrogen increase crop yield?). Effect size tells us the biological significance (how much does crop yield increase given a level of nitrogen addition?). This is the main focus in medicine. What is the increase in odds of survival for a new drug? And R² tells us how much what we’re studying explains vs the other sources of variation (how much of the variation in crop yield is due to nitrogen). It tells us how close we are to done in understanding a system.  I am not biased. I like all three summary statistics (and the different modes of scientific inference that they imply).

But if you ask me how they are used in ecology, then I think the answer is pretty clear that the p-value is way over-emphasized relative to the other two. You can find dozens of papers making this same claim (e.g. this and this). But the one that really pounds this  home to me is this 2002 paper by Møller and Jenions. In this paper they conduct a formal metanalysis of a random subset of papers published in ecology journals and look at the average R² across these papers. Anybody want to guess what it is? We know it won’t be 80% or 90%. Ecology lives in a multi-causal world with many factors influencing a system simultaneously. Maybe 40% might be reasonable? Nope. 30%? Nope. At least 20%?! No. Depending on the exact method it is 2-5%! To me this is astonishing. Papers published in our top journals explain less than 5% of the variance (UPDATE: see footnote). In a less jaw-dropping result but very much In the same vein,  Volker Bahn and I showed that we can predict the abundance of a species better by using spatial autocorrelation (basically copying the value measured at a site 200km away) then by advanced models incorporating climate, productivity, land cover, etc.

Whether you are motivated by basic or applied research goals, it seems clear that we ecologists need to do better than this! To be very specific we need to deliver on the predictive aspects of science that care about effect size and R2. From an applied side, policy makers and on-the-ground practitioners looking for recommendations for action care almost entirely about effect size and R2. Knowing that leaving retention patches in clear-cut forests increases species richness on average by 10 species (a large effect size) is the main topic of interest. As an additional nuance, if we further know that retention patches only explains 10% of the variation in species richness between cutting sites because it mostly depends on the history of the site and chance immigration events and weather in the first year of regrowth, then at a minimum we need to do more work and we might just pass on taking action. Knowing p is pretty immaterial once a certain credible minimum sample size threshold is passed. From a basic research side, there are also good arguments for focusing on effect size and R². I don’t really believe science is about saying “I can show factor X influences measurable variable Y with less than a 5% chance of being wrong” and I don’t think most other people do either.  I am a big fan of Lakatos, who rejects Popper’s emphasis on falsification and suggests that the true hallmark of science is producing “hitherto unknown novel facts” (elsewhere he raises the bar with words like stunning and bold and risky) and I would agree. Lakatos gives the example of Einstein’s general theory of relativity truly being accepted when the light of a star was observed to be bent by the gravity of the sun – a previously unimagined result. Ultimately, if all we’re doing is post hoc explanation, it is at best a deeply diminished form of science. And even if one is rooted in the innate value of basic research, at some purely practical level there has to be a realization that if ecology as a whole (not individual researchers) doesn’t in some fashion step up and provide the basic tools to help us predict and navigate our way through this disastrous anthropogenic experiment known as global change, then society just might decide we deserve a funding level more like what the humanities receive.

So assuming you bought my above two arguments that:

• Ecology is bad at prediction
• Ecology needs to get better at prediction

then what do we do?

This question is going to be the topic of a series posts (currently planned at three). In this post, beyond introducing the topic of prediction in ecology and arguing that we need to do a better job (i.e the half of the post you just read), I want to examine one major roadblock to getting better at prediction in ecology, what I provocatively called in my title the “insidious evil of ANOVA”.

Now I want to be clear I have nothing against analysis of variance per se. It is a perfectly good technique for putting statistical significance on regressions. And indeed the basic ANOVA-derived F-ratio test on a univariate regression gives the same p-value as a t-test on the slope and has much in common with likelihood ratios (and hence with AIC*) for normally distributed errors (the –log likelihood of normally distributed errors is nothing more than a constant times the sum of squares and hence a likelihood ratio is a ratio of sums of squares just like an F-test barring a few constants and degrees of freedom). So to take away ANOVA sensu strictu you would have to take away most of our inferential machinery. And variance partitioning (including R2 that I am promoting here) is a great thing. I have published papers that use ANOVA and will continue to do so.

What I object to is how ANOVA is typically applied and used (Click here for a humorous detour on ANOVA), starting from the experimental design and ending with how ANOVA is reported in journals. I’ll boil these down to two “evils” of traditional use of ANOVA:

1. ANOVA hides effect sizes and R² – Again, in a technical sense, ANOVA is just the use of an F-statistics to get a p-value on a regression. And you can get R² and effect size off of a regression. But in a practical sense as commonly used (and in every first year stats class), ANOVA specifically means a study where you have a continuous dependent (Y) variable and one or more discrete, categorical independent/explanatory/X-variables. The classic agricultural example is yield (continuous) vs. fertilizer added or not added (discrete). Or abundance of target species in the presence and absence of competition. There is again nothing per se wrong with this. Its just that most software packages out there (including R for the aov command) only report a p-value when you run this kind of ANOVA. They don’t report an effect size (difference in mean yields for with vs without fertilizer). And they don’t report an R². You can get these values out with a little extra work but they’re not in the default reports. And then reviewers and editors let the authors write the ms reporting only a p-value without an R². This is how we end up with a literature full of p<0.00001 but R2=0.04. I would argue that every single manuscript should be required to report its R² and effect size. I hypothesize this requirement alone would cause the average R² of our field to go up. At least some people would be embarrassed to publish a paper with an effect size of 2% or an R² of 3%. It would be painful, because this is the state of our field today, but it would be really healthy in the long run to mandate always publishing an R² and an effect size alongside the p-value.
2. ANOVA experimental designs focus on the wrong question – A typical ANOVA setup asks the question does X have an effect on Y. In ecology it is not surprising                                      that more often than not X does have an effect on Y (everything has an effect on Y when Y is something like abundance or birth rate or productivity). Indeed it would be shocking if X did not have an effect on Y. At that point it just becomes a game of chasing a large enough sample size to get p<0.05 and then walla! its publishable. Instead we should be asking “how does Y vary with X”. This doesn’t require a drastic change in the experimental methods. Just a shift in thinking to response surfaces instead of ANOVA. A response surface measures Y for multiple values of X and then interpolates a smooth curve through the data. This is just as accessible as ANOVA – specifically it does not require an a priori quantitative model. However, it sure feeds into formulating new models or testing models somebody else developed. There was a nice recent review paper on functional responses by Denny and Benedetti-Checchi that shows how powerful having a response surface is in ecology (although they focus on mechanism and scaling rather than statistics and experimental design). Having a tool and mindset  that are more focused on prediction leads directly to questions of R² (how big is the scatter around our line) and effect size (how much does the line deviate from a flat horizontal line) AND we get something drives us immediately to models and we get a quantitative prediction (albeit phenomenological) even before we have a mechanistic model. This is a no-lose proposition.

A few technical details and an example will make response surfaces more clear. One reason response surfaces have been limited in use is that they traditionally required using NLS (nonlinear least squares regression) unless the response surface was a boring straight line, but in this day and age of GAM (basically spline regression) this excuse is gone! The figure below shows a contrast between traditional ANOVA approach (the boxplot in subfigure A) and response surfaces (subfigure B and then a 2-D version in subfigure C). Other than a shift in mindset (plot a spline through the data instead of a box plot), the only practical implication is that we ought to emphasize number of levels within a factor (e.g. four levels of nitrogen addition or competition instead of just the two levels of control and manipulation). This can be cost free because we can reduce the number of replicates at each level proportionately (i.e. 4 levels with 2 replicates instead of 2 levels with 4 replicates) (again compare subfigure A with subfigure B).

Just to expand briefly on the benefits of a response surface, it serves as a wonderful interface to modeling. If we have a model, we can test if it produces the response surface found empirically; if we don’t have a model it immediately suggests phenomenological models and may even suggest mechanistic models (or at least whether the positive or negative feedbacks are dominating and whether there is an optimum). Further we have a prediction immediately useful in a applied context. If we have a response surface of, say, juvenile survival vs. predator abundance, we can immediately have an answer for that conservation biologist who says, given that I have limited dollars, what kind of benefit will I see if I invest in eradication of the invasive predator? Being scientists, we will immediately want to caveat this analysis with warnings about context dependence, year-to-year variation etc. That’s fine, but I bet the conservation donor will still be a lot happier with you if you have this response surface than if you have p<0.05! So, there are both basic and applied reasons to use response services.

Of course there is lots of fine work in ecology that addresses both of my concerns. But without doing a formal meta-analysis I am pretty sure that the version of ANOVA I am picking on is a plurality if not an outright majority of studies published in major ecology journals. Occasionally the independent variable truly is categorical and unordered so a response surface won’t work, but this is rare and even then can often be improved to a continuous variable with a little thinking (and it doesn’t excuse not reporting a measure of goodness of fit and effect size!).

In conclusion, I did not get into science to conclude “Factor X has an unspecified but significant effect on factor Y”. This is all the traditional use of ANOVA tells us. Two simple proposed changes: 1) require reporting the R² and effect size to publish and 2) shift to a response surface mentality (specifically more levels with fewer replicates and fitting a surface through the data) lets us go past this question. Now we can ask “how does Y vary with X and how much of Y is explained by X?”. This is much more exciting to me and I hope to you! This subtle, labor cost neutral, but critical reframing lets mechanistic models in the door much more quickly and gives an ability to answer applied questions in the meantime. The opportunity cost of failing to do this is what I call “the insidious evil of ANOVA”. I am convinced that our field would progress much more quickly if we made this change. What do you think?

*don’t get me started on AIC – that is for another post, but note for now that focusing on AIC neatly dodges having to report an R2 and effect size

Footnote from Jeremy: Upon reflection, Brian and I have decided we ought to alert readers that Anders Møller has been subject to numerous very serious accusations of sloppiness and data falsification, one of which led to retraction of an Oikos paper. See this old post for links which cover this history. We leave it to readers to decide for themselves whether that history should affect their judgment of a paper (Møller and Jenions 2002) that has not, to our knowledge, been directly questioned. In any case, Brian and I believe that his post is robust: many R2 values reported in ecological papers are indeed low, few are extremely high, and the point of the post does not depend on the precise value of the average R2.

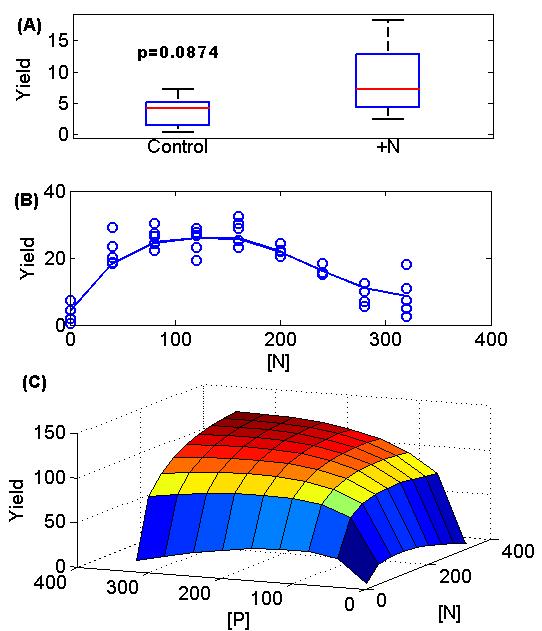
This figure shows classic agricultural yield data based on amount of fertilization. Data from Paris 1992 (The return of Von Liebig’s “Law of the Minimum”) with some random noise added by me. A) A traditional ANOVA approach showing yield vs. nitrogen addition with only two or a few levels. Here there is borderline non-significance (p=0.08). B) The much more revealing response surface (it turns out this data was from the 0 phosphorous addition set of the data and the plants actually fare poorly when too much nitrogen is added without phosphorous). C) The full fitted 2-D surface of yield vs nitrogen and phosphorous. The Paris paper actually fits different functional forms to test whether Liebig’s law of the minimum is true or not. This is a far cry from (A)!