The fitness landscape of beer: Fisher’s geometrical model vs. IPA

This is a silly post with two serious points:

1. Sometimes, even really abstract mathematical models can make really good predictions about real-world biology. Further, they can do so because of their abstractness, not despite it.*
2. A prime virtue of mathematics is that it forces us to be precise–in our assumptions, in our conclusions, and in the logic by which we derive our conclusions from our assumptions.

I’ll make these points by introducing you to one of the most abstract–and yet empirically successful–mathematical models ever produced in biology. But I doubt that many of you would voluntarily read about abstract mathematics. So let’s start by talking about beer instead. 🙂

India pale ale (IPA) is a style of beer first brewed in Britain in the 19th century. It’s hoppier than regular ale (for non-beer drinkers: hops make beer bitter). The usual story is that India pale ales were first brewed for shipment to India, and were brewed much hoppier and higher in alcohol than regular ales in order to preserve them for the long journey. But many people found the hoppiness tasty, and so IPA remained popular even after the invention of preservatives and the advent of faster shipping methods.

But according to Wikipedia, the usual story isn’t true. In fact, what we now call IPA was indeed a hoppy beer, but it was originally for domestic consumption, and was just one of a number of ales that the Bow Brewery exported to India. Other styles of beer survived the trip to India, although IPA may have survived it better than most, and was also popular with East India Company traders. Other brewers started copying the style when they entered the Indian market to compensate for the loss of the Russian export market due to Russian tariffs. So IPA wasn’t actually a “hopeful monster“. It’s not that somebody brewed the world’s first really hoppy beer purely for the sake of preserving it for a long journey, and through an incredible piece of luck found that people actually liked the taste.

But we don’t just have to rely on Wikipedia. A highly-abstract evolutionary theory explains why the usual story is implausible. (C’mon, you’ve come this far–keep reading! There aren’t even any equations!)

The theory is Fisher’s geometrical model (aka Fisher’s geometric model). It’s maybe the most abstract, elegant argument in all of evolutionary biology except for the theory of evolution by natural selection itself. Originally, it was a formal metaphor for the process of adaptation via mutation and selection. Fisher was trying to model what he called “the statistical requirements of the situation”.

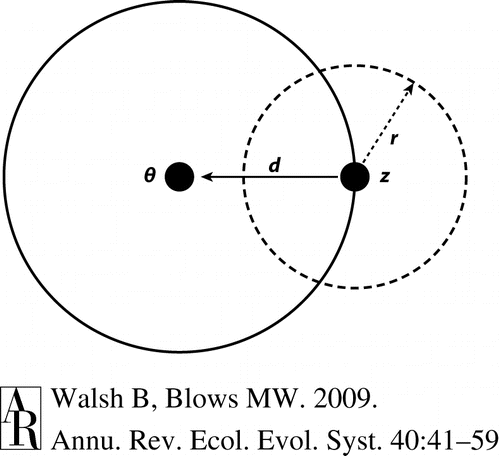
Here’s the original model (what follows draws heavily on a comment I once left on another blog).** Imagine that the phenotype z of an individual organism can be described as a point in a 2-D space (the argument generalizes to any number of dimensions). Now imagine that there’s some optimal (fitness-maximizing) phenotype theta, which is some distance d away from the individual’s phenotype. The smaller d is, the closer the phenotype is to the optimum, and so the higher the organism’s fitness. A mutation changes the phenotype, moving it some distance r in the 2-D phenotype space, in a random direction (a random direction because whether or not a mutation occurs has nothing to do with its fitness effect). You can think of r as the effect size of the mutation; a mutation of large effect is one producing a big phenotypic change (large r). A beneficial mutation is one that moves you from z to some point closer to the optimum phenotype, a deleterious mutation is one that moves you further away. It can be shown that, the smaller r is (i.e. the smaller the mutation’s effect on phenotype), the more likely it is to be beneficial. In the limit of very small r, the probability that a mutation is beneficial approaches a maximum of 50% for a 2-D phenotype. Conversely, mutations of large effect are very unlikely to be beneficial. Even if they move the phenotype in the general direction of the optimum, they can overshoot the optimum and so can leave the phenotype even further from the optimum than it was before. Small mutations reduce the possibility of overshoots, which is why they’re more likely to be beneficial.

Here’s a figure from a recent review, illustrating what I just said:

All of which explains why the usual story about IPA is highly implausible. In the usual story, the flavor of British ales presumably was already nearly optimized. The odds are really low that a big random change would improve their flavor! Not because of anything to do with brewing, but because of geometry.***

Now, you could argue that while it’s nice to have a formal proof of that intuition, the intuition itself is fairly obvious. When you’re close to a mountaintop, there’s almost nowhere to go but down. That’s kind of obviously true, whether you’re talking about actual mountaineers, or metaphorical mountaineers like living organisms or beers. Although I suspect it’s one of those things that’s only obvious ex post, not ex ante. Heck, until it’s pointed out to you, is it even obvious that you can think of an organism’s phenotype as a point in a multidimensional space in the first place? That’s not even really a simplifying assumption, like the old joke about assuming a spherical cow. It’s not an approximation you make in order to solve the problem–it’s an abstraction you make in order to define what the problem is. The genius of Fisher’s geometrical model isn’t in how it answers the question–the genius is in what question it asks. Fisher’s geometrical model answers a biological question not by modeling biology, but by not modeling biology. It recognizes that the biological question is just a specific instance of a much more general and abstract geometrical question.

But Fisher’s geometrical model does more than just confirm a possibly-obvious intuition. For instance, the model also makes non-obvious predictions about how the phenotypic “dimensionality” of the organism affects the probability that mutations of any given effect size will be beneficial. It turns out that there’s a “cost to complexity”–beneficial mutations are less likely, and adaptation slower, for organisms with higher-dimensional phenotypes. And it turns out you can’t avoid paying that cost of complexity by having a “modular” phenotype (see Orr 2005 for review, and see Tenaillon [forthcoming] for another review).

You can also extend Fisher’s geometrical model in various ways, in particular by drawing on another abstract bit of mathematics known as extreme value theory. Extensions of Fisher’s geometrical model consider everything from the evolution of sex, to the evolution of development, to adaptation in changing environments, to species hybridization, and more (again, see Orr 2005 and Tenaillon [forthcoming] for review, although there’s a lot of subsequent work–this is a hot area of research). And experiments testing the predictions are starting to come out (e.g., Gifford et al. 2011, Bataillon et al. 2011). So this is not a bunch of mathematicians getting excited about abstract models that are divorced from the wonderful messiness of reality. Rather, it’s a matter of mathematicians and empiricists getting excited about abstract models because those models are telling them so much about reality. A reality that turns out to be much less messy than you might’ve thought, if you look at it in a sufficiently abstract way.

As an aside, you can also ask many of the same questions by starting from a much less abstract and more specifically-biological observation: genes consist of sequences of four nucleotides, and mutations convert one gene sequence to another. It turns out that such “mutational landscape models” make predictions quite similar to those made by Fisher’s geometrical model (Orr 2005). It’s interesting to think about the connections between more- and less-abstract models of the same phenomena. Steven Frank has a wonderful new paper coming out on this, and it’s something I plan to blog about in future.

To make my second point, about the value of precision (as opposed to abstraction), I’ll consider something that Fisher originally got wrong. Fisher thought his geometrical model implied that adaptation would be based on mutations of small effect. After all, mutations of large effect are highly unlikely to be beneficial, much less likely than mutations of small effect. But just because mutations of large effect are unlikely to be beneficial doesn’t mean that adaptation won’t be based on such mutations. That’s because mutations of small beneficial effect are far more likely to be lost to drift than are mutations of large beneficial effect, a point first recognized by Kimura. But even that’s not the end of the story, because the expected distribution of effect sizes of mutations fixed during a single “step” of adaptation isn’t the same as the expected distribution of effect sizes of mutations fixed during an entire “adaptive walk” towards an optimum phenotype. Recent work derives quantities like the expected distribution of effect sizes of mutations that will be fixed during an adaptive walk, the expected effect size of the mutation fixed during the ith step of an adaptive walk, the expected number of “mutational steps” required to complete an adaptive walk, etc. Recent work thus resolves apparent discrepancies between Fisher’s original geometrical model and empirical data on “quantitative trait loci” (QTLs) indicating that beneficial mutations of large effect often make an important contribution to adaptation in real organisms (Orr 2005). So it’s not that Fisher’s original geometrical model is “wrong” in the sense that QTL data falsify it. Rather, it’s that comparing Fisher’s original geometrical model to QTL data is an apples-to-oranges comparison. If you want to predict the distribution of effect sizes of mutations fixed during an adaptive walk, then you need to extend Fisher’s original geometrical model so as to predict that distribution–not the distribution of some other quantity. Not even some other seemingly-similar or closely-related quantity.

Fisher’s mistake was one of imprecision. He mistook one result–the distribution of fitness effects of mutations as a function of their effect size–for a subtly but importantly different result–the distribution of fitness effects of mutations that will be fixed during an adaptive walk. This is a very easy sort of mistake to make, even for theoreticians.**** Orr (2005) emphasizes that both Fisher and Kimura–two of the greatest evolutionary theoreticians ever–both drew incorrect “take home” conclusions from mathematically-correct derivations. If they can make this sort of mistake, anyone can.

So while I still think that there’s such a thing as good hand waving, I think it’s rare. I’ve increasingly come to think that progress in ecology depends on ecologists relying less and less on hand waving verbal arguments, and more and more on mathematics. The history of research on the genetics of adaptation is a great illustration of what’s possible when you rely on mathematical models (here, highly abstract models), and when you’re very careful to model precisely the quantity of interest. As opposed to modeling something that’s sort of related to the quantity of interest and then waving your hands about how it’s hopefully close enough. Because that’s like trying to turn an apple into an orange by waving your hands.

*I’m not saying that highly abstract models are the only models that are useful. See this old post for a discussion of the value of non-abstract models.

**Here and throughout the post I gloss over technical details, taking the view that that’s what the primary literature is there for. The papers I link to provide a gateway to that literature. I’m just using Fisher’s geometrical model to make some broad points I think are worth making, and also to encourage readers to read up on it. I’m not trying to provide a precise technical summary of research in this area.

***Do not hassle me about the possibility that the “fitness landscape” of beer has numerous local optima, or is mostly flat, or etc. I’m trying to keep things simple here.

****A colleague who works on this stuff once summarized a paper of Allen Orr’s to me as saying “Everybody please stop misinterpreting my models.”